P vs NP, Logic and Philosophy Behind Computation

This is my First Article, Here I try to present Intuition and foundational philosophy of computation to CS and non-CS students alike. I try to make the theory as simple as possible but not simpler that takes the aesthetics away. references are mentioned at footer.

What is computation?

Computer science isn’t just limited to computers and electronic devices. Famous Computer Scientist Edsger Dijkstra once said, “computer science has as much to do with computers as astronomy has to do with telescopes”. like the natural sciences, computer science also has a solid philosophical background.

quoting Scott Aaronson “computer science is a mathematical set of tools, or body of ideas, for understanding just about any system—brain, universe, living organism, or, yes, computer. ”

A Physicist seeks out “The rules of nature, with varying scale from subatomic to cosmic and often It happens by finding a general rule, and then they will try to find deeper rules that makes the general rule stable in a top-down approach”.

A Computer scientist seeks out “How hard is the system built by these rules? we typically take stable simple systems and try to form more complex systems in a bottom-up approach”. There is also a fundamental question that drives a computer scientist, “why some problems are Harder than others?” and we try to look for mathematical structures, logical models that helps us in interpreting the problems and try to solve them (or) gain Intuition along the way.

But what is Hardness? we had to give a metric to classify some problems as hard while others as relatively simple and also is every problem solvable?The answer to the second question is, “NO”. let’s try to formalize this, for that let’s have a brief about turing machine, “Turing machine is an abstract mathematical model that takes an input, performs some basic operations, writes output and halts (stops)”. computers are built with the notion of turing machine ( but not perfectly because computers have finite memory while turing machine is theorized to have infinite memory ) but any computer can be converted to a Turing machine. There are many variants of Turing machine but each of them can be converted to a deterministic Turing machine with more time penalty.

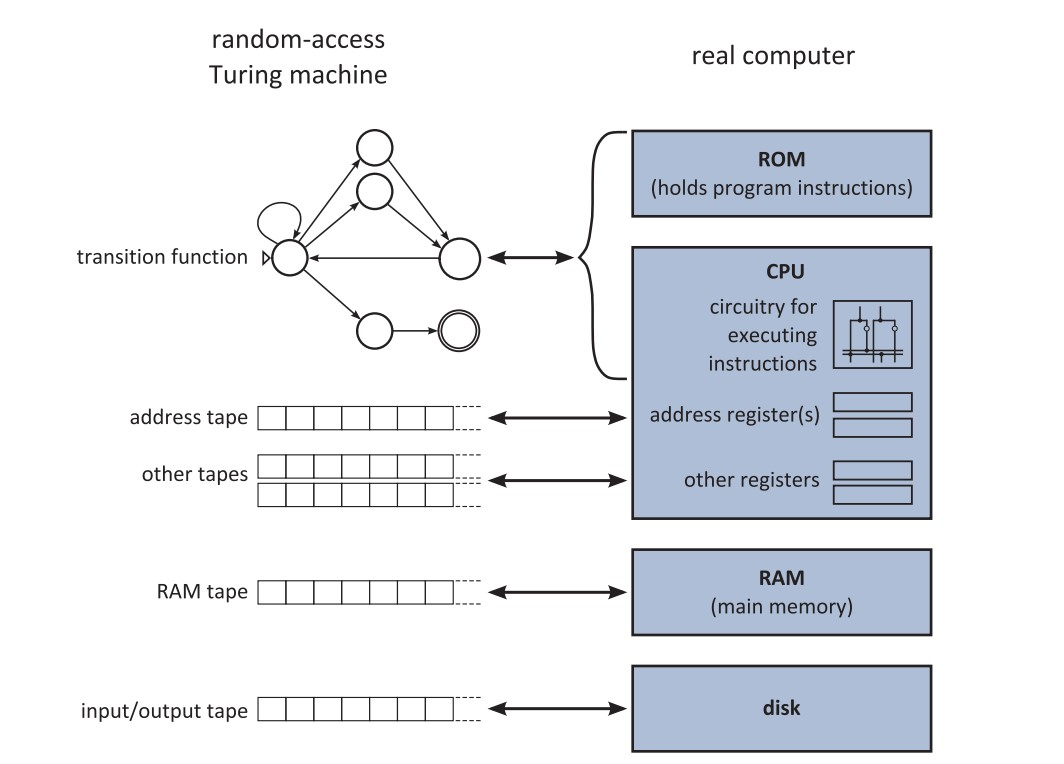
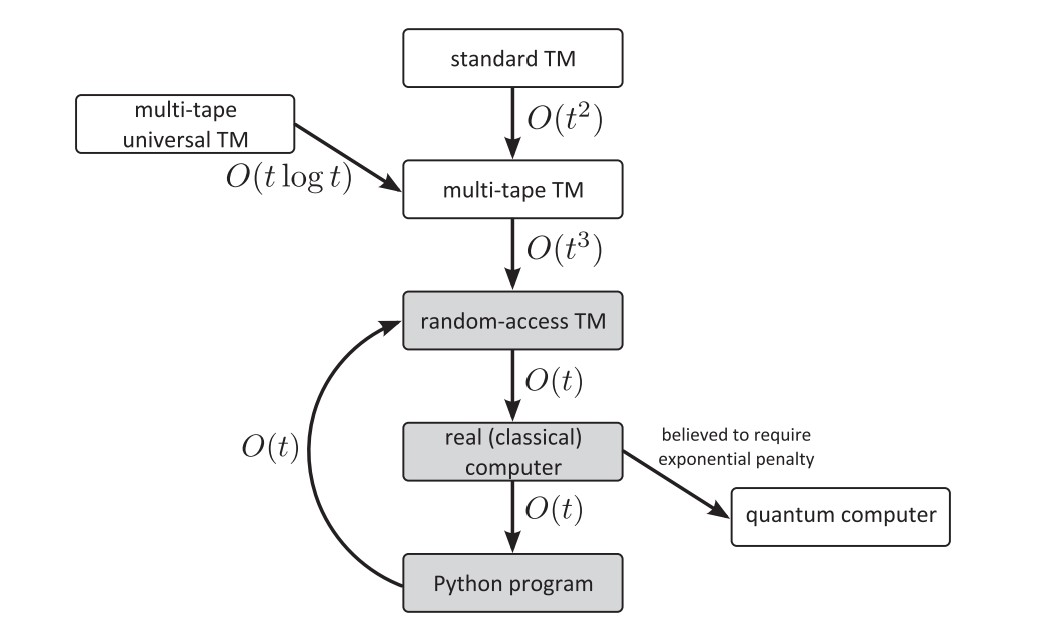
So, As the turing machines are very powerful, we take turing machine as the computational model for computational theory and complexity theory.

To solve a problem, we take input perform operations and create an output. the set of all possible inputs of the problem is called a “language” mostly infinite. a language is called decidable, If a turing machine can output “Yes” or “No” and halt on every input from the language.

Tracing back, some problems are inherently Unsolvable ( Undecidable ), one such is the infamous Halting problem.Halting problem is an undecidable problem where given a turing machine description, input, we should determine whether the turing machine halts on that input. like a general algorithm that can determine whether a turing machine halts or goes into an infinite loop on an input. there is a nice proof to prove this via contradiction, but I’m not explaining it as it doesn’t help in our P vs NP quest.

So, Tracing back Answering the first question, we classify the problems by their factors like solvability, time requirement, space requirement, computational model.

Here, I need to specify the difference between a deterministic turing machine, non-deterministic turing machine. in essence, determinism here specifies being able to do only one operation at a time, in non-determinism you perform correct operation at every instant without searching through possibilities. in reality, non-deterministic machines aren’t possible. but as we said earlier, every non-deterministic turing machine can be converted into a deterministic turing machine with time penalty.

Complexity classes

moving on,

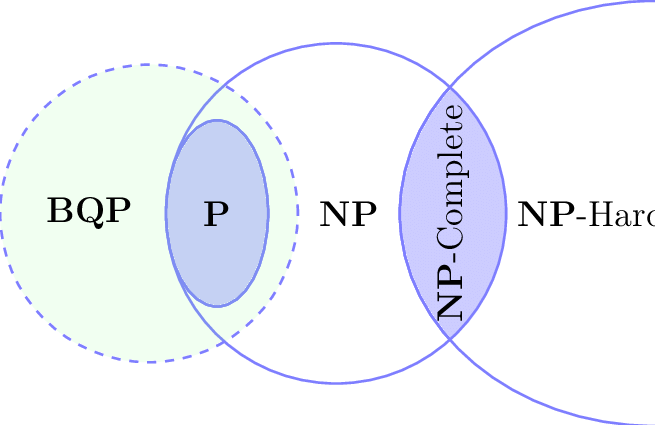
P is the set of all problems that can be solved in polynomial time ( at most N^k) on a deterministic turing machine where, N is the length of input, k is a constant.

NP is the set of all problems that can be solved in polynomial time ( at most N^k) on a non-deterministic turing machine.

key thing to note here, is that every NP class problems can be solved in exponential time at most ( at most 2^(N^k) ) time on a deterministic turing machine.

EXPTIME is the set of all problems that can be solved in exponential time ( at most 2^(N^k)) on a deterministic turing machine.so, NP ⊆ EXPTIME

NP-complete is the set of NP problems which can be converted to every other NP problem can be in a polynomial time penalty. If we want to prove one NP problem as NP-complete, we need not to prove every NP problem being reduceable to that problem we can just prove that NP problem can reduced into NP-complete. Note that above, I used convertible, reduceable interchangeably.

the hierarchy,

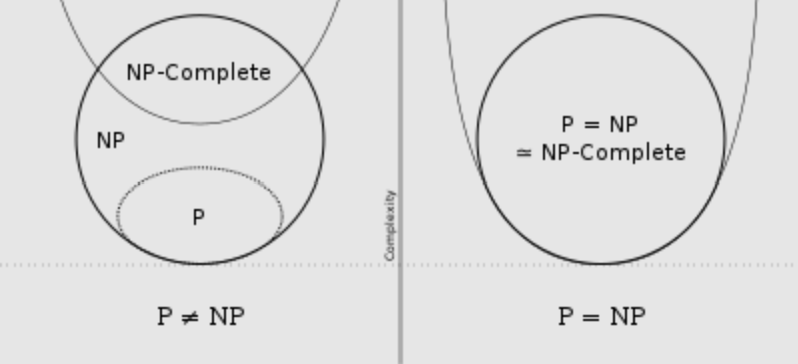
there are also, other complexity classes like NP-Hard ( problem set to which every NP problem can be reduced to whether NP or not ), PSPACE ( analogous to P in space ), NPSPACE ( analogous to NP in space ), before defined EXPTIME ( NP ⊆ EXPTIME ), NEXPTIME ( analogous to EXPTIME for NDTM ), etc. but we don’t need them to introduce P vs NP.

One Important thing to note, is even though NP problems require exponential time to solve, they require only polynomial time to be verified. i.e, we can think P class problems are easier to solve, easier to verify and NP problems are harder to solve but easier to verify.

Even though we aren’t able to prove P vs NP

But with time hierarchy theorem, we proved that, P ⊊ EXPTIME ⊊ 2-EXP ⊊ ... and NP ⊊ NEXPTIME ⊊ 2-NEXP …

which can be helpful in solving P vs NP.

P vs NP ( the holy grail of computer science )

P vs NP is about figuring out whether P = NP or P ≠ NP. It’s is not just a mathematical problem but a philosophical one, “Is finding solutions harder than verifying them?” ( since P class problems can be solved easier, NP class problem are verified easier ).

we might think intuitively, “finding solutions is harder than verifying solutions” like “writing a great poem should be harder than checking a great poem”. Even the famous physicist Feynman had trouble even being convinced that P vs. NP was an open problem!

Because, All NP problems require brute-force search ( searching all possible states for solution ) which results in the exponential time requirement. So to believe P = NP, we need to assume there is a general efficient way to solve every NP problem. which is also a hard thing to assume against our Intuition.

we generally believe the conjecture that P ≠ NP but It’s very HARD to prove it!!

because, “A fundamental challenge when proving P ≠ NP is that, we have to separate NP problems that are actually HARD from the problems that just look HARD or used to be assumed HARD”. problems like primality testing, DNA sequencing which were assumed to be NP are now in P. the proofs that tried to prove, P ≠ NP can be rejected with this simple reason. as If we were to believe they work, then these polynomial reducible problems shouldn’t exist in the first place!

We can however reduce scope to make our proof more stable, here NP-complete comes into picture. remember that any NP-complete problem can be converted into any NP class problem. so, If we’re able to prove one NP-complete problem is equal to (or) not equal to P. we prove all problems of NP are equal to (or) not equal to NP.

Repercussions of proving P = NP are massive, If P = NP many other complexity classes fall into P as well like co-NP, Πk P, Σk P.

with P = NP,

any reasonable length mathematical proof can be found efficiently by an algorithm! ( because even though in polynomial N^k, if the k is big It would be inefficient ).

the idea that such problem is in NP was actually pointed out by Kurt Godel in his 1956 letter to von neumann. he wrote, “Consider the problem of deciding whether a mathematical statement S has a proof in F with n symbols or fewer. we could always just program a computer to search through all 2^n possible bit-strings with n symbols, and check whether any of them encodes a valid F-proof of S.”

Godel also pointed out, “it’s far from obvious how to prove that there isn’t a muchbetter approach: an approach that would avoid brute-force search, and find proofs of size n in time polynomial in n”. essentially discussing, proving P ≠ NP is HARD. the formal conjecture of P vs NP was formulated by cook in his 1971 paper.

P = NP will also mean AI would be perfect as we can simply search large tree of possibilities in polynomial time. VLSI designers can design optimum circuits with minimum power requirements. any scientist can obtain the simplest theory that explains his/her experimental data, by Occam’s razor this is supposed to be the correct one!

as said earlier in summary, “Any problem whose solution that can be verified easily, can be produced approximately that much easily”.

It may also rule out the need of randomized algorithms, stochasticity principle as the gains will be negligible.

On the other hand, all our cryptographic algorithms are designed with the assumption of existence of one-way functions which in turn assumes P ≠ NP. so, there can be trivial decoding algorithms for every cryptographic algorithm, causing vulnerability to our security, privacy, data integrity.

so, this is the explanation I felt sufficient for intuitively understanding complexity. because, I saw even experienced people having confusion over these ( cough cough tutorialspoint guy ).

the main intention of writing this article, is to introduce these concepts intuitively to wider audience and to give motivation to CS students that they’re doing something really fundamental than just programming stuff. sadly, I was introduced to these concepts just before couple of months in my final year of Btech. had I been introduced to these earlier, It might’ve had significant impact in my formative years of undergraduation. which I hope happens to someone else. remember to get away from your engineering lens to a scientist lens once in a while.

an engineer will accept the rules they’re given and try to solve problems with those rules, a scientist will question the rules itself. a mechanical engineer may design machines without realizing that forces are illusion but a physicist would realize that. similarly, a software engineer will develop algorithms without realizing the underlying assumptions.

there are potential things that I missed (or) trivialized above for better understanding. as I’m fairly inexperienced, if there’re any errors above feel free to point out by my twitter handle.

References:

1. Introduction to the theory of computation - M Sipser
2. The history and status of P versus NP Question - M Sipser
3. Computational complexity a modern approach - S Arora, B Barak
4. The nature of computation - C Moore, S Mertens
5. What can be computed? - J MacCormick
6. Why Philosophers Should Care About Computational Complexity - S Aaronson
7. Quantum computing since democritus - S Aaronson
8. Automata, Computability, and Complexity, MIT 2011 - S Aaronson